The following organizations and institutions are duly acknowledged for funding and supporting our research:
European Union (EU) Organizations:

Swedish Organizations:
Project: Modeling and Analysis of Random Spatial Systems for 5G Networks (EU-H2020-MARSS-5G)

Keywords: 5G Networks, V2X Communications, Autonomous Vehicles, Network Modeling, Road Safety
Fellowship: Marie Sklodowska-Curie Individual Fellowship
Program/Call: H2020-MSCA-IF-2014
Grant No.: SEP-210186649
Reference No.: 659933
Host:

Division of Communication and Antenna Systems (CAS),

Dept. of Electrical Engineering, Chalmers University of Technology, Göteborg, Sweden
Start Date: Sep. 07, 2015
EU Website: https://cordis.europa.eu/project/id/659933
Chalmers URL:

https://research.chalmers.se/en/project/?id=6579

http://www.chalmers.se/en/projects/Pages/Modeling-and-Analysis-of-Random-Spatial-Systems-for-5G-Networks.aspx 
Overview: 

Smart cities with autonomous vehicles will result in "sustainability" through: (i) a decrease in road-accidents; (ii) the amelioration of traffic fluidity; (iii) less dependence on traditional traffic lights and infrastructure; (iv) a minimization of wasted resources and mobility spending, and (v) a decrease in pollution level. The ultimate objective of our research is to make an autonomous vehicle " smart" and "ultra-reliable" enabled with 5G/B5G Communications. Due to the enormity of this undertaking, we only focus on carefully investigating the critical use-case of the four-way intersection, where the objective is to make the network of vehicles around the intersection "intelligent" through RF connectivity. In particular, we want to explicitly understand the reliability of communication as vehicles navigate around the intersection. Below, we briefly explain the three key components of this research track.

 

● Intersection Use-Case: The 4-way intersection use-case is a critical scenario of major consequences to road-safety, well-being, productivity and sustainability to society. The figures below visually show and describe the importance and transportation challenge of intersections.

 

Fig.1a - Vehicular collision at intersections consist nearly 47% of all road accidents combined.

Fig.1b - Intersections are the leading cause for traffic congestion in cities. As a result, drivers are generally spending 40% in the car idling during gridlock.

● V2X Communications: Technologies such as Lidar, sensors, cameras, infrared vision are important for making a self-driving vehicle dependable and safe. However, in certain situations, such systems are simply insufficient to cope with the reality of road transportation. One such instance is the challenge of "blind-intersections" in a metropolitan environment. As shown by the figures below, V2X radio communication are practical for seeing around built-up corners. Alternatively, V2X systems can also serve as a necessary redundant sensing technology used to detect and avoid collisions with other nearby vehicles, cyclists, pedestrians, and random objects.

 

Fig.2a - Lidar system mounted on vehicles is a key technology for autonomous capability.

Fig.2b - Lidar and radar systems have safety-critical limitations. Most notably they fail to see incoming vehicles "around corners" as the view is obstructed by infrastructures and buildings.

Fig.2c - Integration of V2X radio system can compensate for the limitations of autonomous vehicles and further improve its overall reliability.

● 5G/B5G Architecture/Networks: The two more critical paradigms of this mobile network technology are 5G-IoT which is key to unlock the potential future of "smart cities"; and the other is 5G-V2X (a.k.a. C-V2X), which will revolutionize intelligent and safe "automotive technology" with self-driving capability. Although IEEE 802.11p/DSRC exists, C-V2X communications is more powerful and sophisticated for use in connected cities, where everything that must be connected (i.e., vehicles, traffic lights, pedestrians, road side infrastructures, and networks) will be connected. The figures below show the use-cases of 5G communications, and the implications that it may have in making an intersection intelligent with vehicular communications and cooperation.

 

Fig.3a - Smart cities and vehicular advancement are some of the exceptional use-cases of 5G wireless communication networks. These innovative technologies will inevitably disrupt traditional vehicular transportation.

Fig.3b - This is how an "intelligent intersection" will look once all vehicles are autonomous and connected. Congestions, traffic jams, delays, and more importantly accidents are drastically minimized, with the ambitious objective of being completely eliminated. 5G will not get us to this, but it is a step in the right direction. Let's get to work!

 
Research: 

It is important to highlight that ~ 50% of all accidents occur at the intersection, and so carefully studying the so-called "intersection problem" is crucial. The following 4 movies (2min each!) show the reliability per random traffic realization as a transmitting vehicle (TX) communicates with a receiving vehicle (RX) while it maneuvers around the intersection. We consider the granular reliability per traffic in a build-up metropolitan and in the suburbs. The results are quite remarkable. Please see our papers for more on the "significance" of what the results really means for real-world deployment on vehicles with autonomous capability.

 

Practical Values for Real-World Analysis Extreme Values for Fundamental Limits/Stress-Test Analysis
Case I: Urban Intersection, Small Road Segment (R = 200 m) Case II: Urban Intersection, Sizeable Road Segment (R = 10 km)

Case III: Suburban Intersection, Small Road Segment (R = 200 m) Case IV: Suburban Intersection, Sizeable Road Segment (R = 10 km)

 

 

Fine-grained analysis using the meta-distribution techniques. For more on this, please see our papers.  

 
Dissemination: 

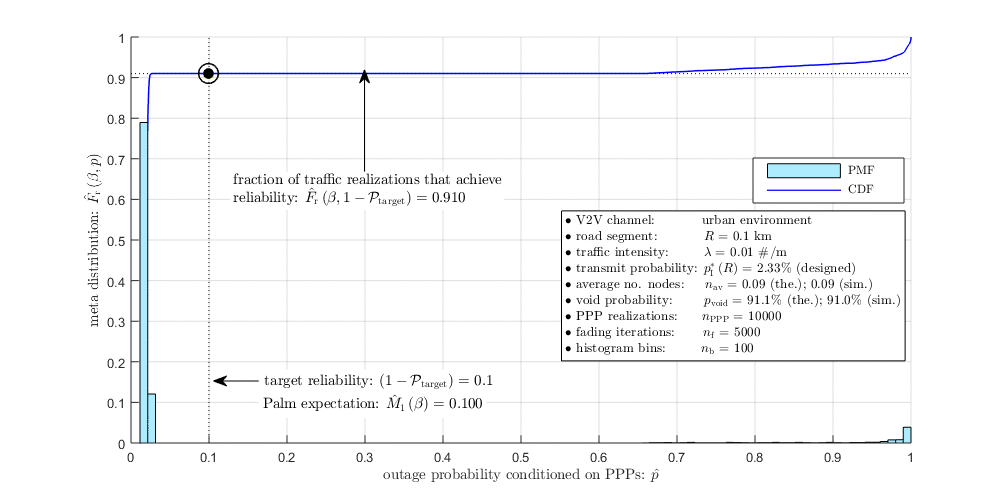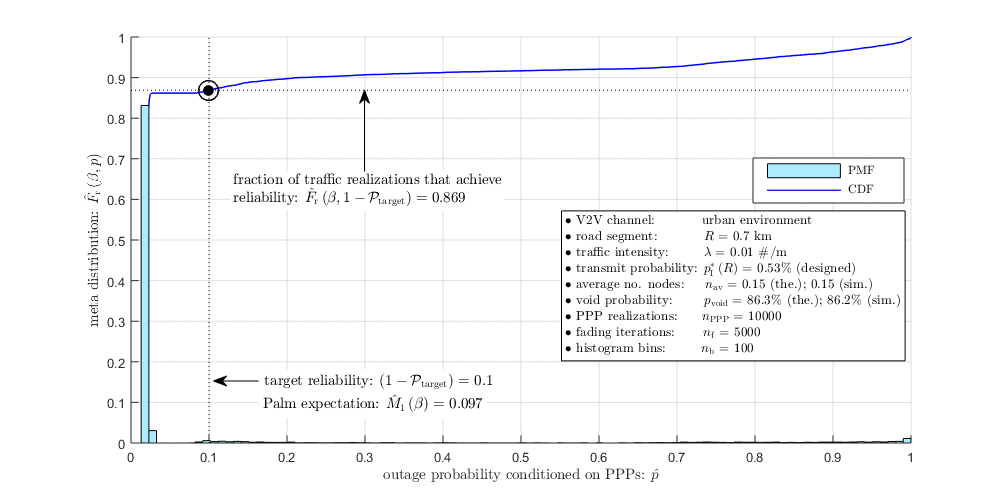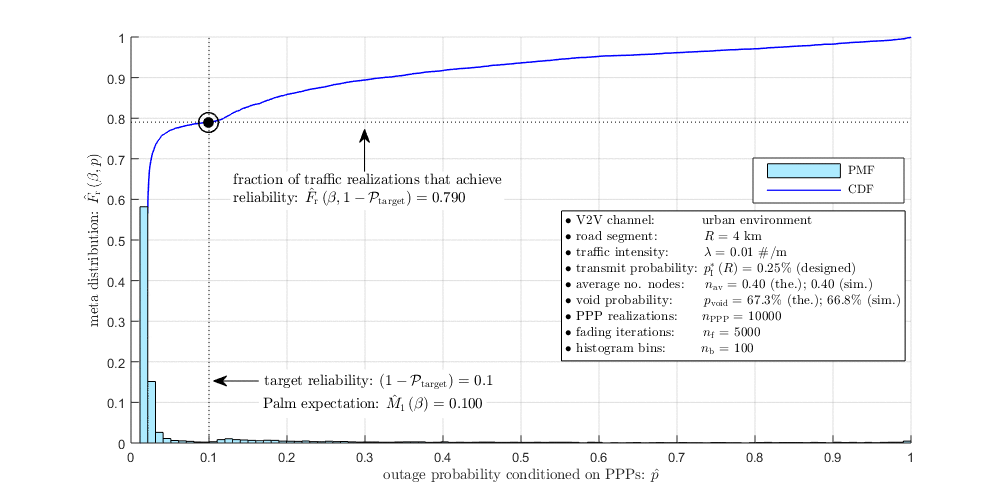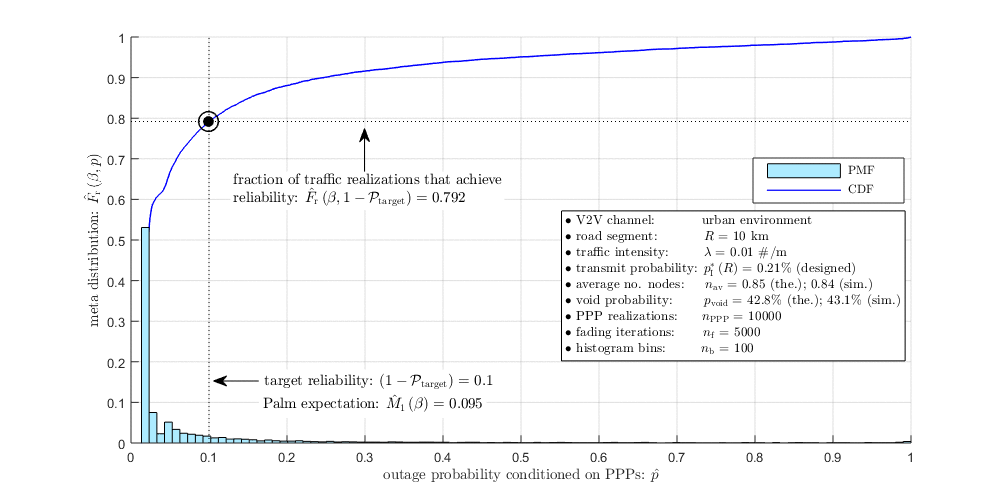
The research of the EU-H2020-MARSS-5G project was disseminated through different means, including: reports, publications, technical seminars, and outreach efforts.

 

● Peer-Reviewed IEEE Publications:

 

□

M. Abdulla, E. Steinmetz, and H. Wymeersch, "Vehicle-to-Vehicle Communications with Urban Intersection Path Loss Models," In Proc. of IEEE Global Communications Conference (GLOBECOM'16), pp. 1-6, Washington DC, USA, Dec. 4-8, 2016.

  

 
□

M. Abdulla and H. Wymeersch, "Fine-Grained vs. Average Reliability for V2V Communications around Intersections," In Proc. of IEEE Global Communications Conference (GLOBECOM'17), pp. 1-5, Singapore, Dec. 4-8, 2017. (related video: )

  

 
□

M. Abdulla and H. Wymeersch, "Fine-Grained Reliability for V2V Communications around Suburban and Urban Intersections," arXiv:1706.10011, pp. 1-27, Jul. 2017. (related video: )

      

 
□

M. Abdulla and K. Wu, "5G Connected Vehicles: the Missing Link to Highly Autonomous Vehicles," Routes et transports Magazine, l'Association québécoise des transports (AQTr), vol. 46, no. 2, pp. 122-127, Oct. 2017. ISSN: 0319-3780 (print)

     

 
□

M. Abdulla and H. Wymeersch, "Vehicular Transmission Reliability over Blind Intersections," IEEE Swedish Communication Technologies Workshop (Swe-CTW'17), Göteborg, Sweden, Jun. 1-2, 2017. (poster session)

       

  

 

 

● Presentation of Technical Seminars: One of the best ways to facilitate knowledge transfer of novel research results is to present and discuss it in formal settings, such as seminars and conferences. As such, we had the opportunity to give many talks on Intelligent Transportation Systems (ITS) across the globe, namely, in: North America, Europe, Middle East, Asia and South East Asia. The interaction with different researchers while giving these seminars made us realize the strong interest and appetite of scholars and professional engineers on all aspects related to the innovative technology of connected and autonomous vehicles. We also benefited to learn the different research initiatives and strategic visions that is taking place in each of these countries and cities that we visited. Overall, we are delighted to highlight that a number of the visited research institutes have demonstrated strong interest in fostering collaboration on V2X communications for autonomous vehicles, where some preliminary work have begun. Below, we give a breakdown of the presented seminars.

 

□ North America — Montréal/Québec/Canadaand Washington, D.C./USA

  • M. Abdulla, "Vehicle-to-Vehicle Communications with Urban Intersection Path Loss Models," Wireless Networking and Control for Unmanned Autonomous Vehicles (Wi-UAV), IEEE GLOBECOM'16, Washington Hilton, Washington DC, USA, Dec. 8, 2016.

  • M. Abdulla, "Les véhicules autonomes," l'École des métiers de l’informatique, du commerce et de l’administration de Montréal - EMICA, Montréal, Québec, Canada, Dec. 23, 2016. [The seminar was in French.] 

  • M. Abdulla, "Self-Driving Vehicles: The Path Forward with LIDAR and V2X Technologies," IEEE VTS/ComSoc/SPS Seminar, McGill University, Montréal, Québec, Canada, Jan. 5, 2017. [Abstract, and Slides are available on the bottom of the page: ] 

  • M. Abdulla, "Pourquoi le Canada est-il en retard dans la course aux véhicules autonomes/connectés, et comment changer cette situation?," l'École des métiers de l’informatique, du commerce et de l’administration de Montréal - EMICA, Montréal, Québec, Canada, Dec. 21, 2017. [The seminar was in French.]

□ Europe/Scandinavia — Sweden

 

 

□ G.C.C. Region/U.A.E. — Dubai and Sharjah

  • M. Abdulla, "Highly Autonomous Vehicles with Connected Capability," Electrical Engineering Dept., College of Engineering and Information Technology, University of Dubai, Academic City, Dubai, U.A.E., Sep. 14, 2017. 

  • M. Abdulla, "Highly Autonomous Vehicles with Connected Capability," Department of Electrical and Computer Engineering, University of Sharjah, University City, Sharjah, U.A.E., Sep. 17, 2017. 

 

□ P.R.China/S.A.R. — Beijing, Shenzhen and Hong Kong

  • M. Abdulla, "Theoretical vs. Experimental Research: How to be a Relevant Telecom Engineer?," Dept. of Electronic Engineering, Tsinghua University, Beijing, P.R.China, Jul. 19, 2017.

  • M. Abdulla, "Fine-Grained Reliability for V2X Communications," School of Electronic Engineering, Beijing University of Posts and Telecommunications (BUPT), Beijing, P.R.China, Jul. 20, 2017.

  • M. Abdulla, "Fine-Grained Reliability for V2X Communications," Dept. of Electronic Engineering, Tsinghua University, Beijing, P.R.China, Jul. 21, 2017.

  • M. Abdulla, "On Spatial Correlation of Shadowing for Movable Small-Cell Networks," Dept. of Electronic Engineering, Tsinghua University, Beijing, P.R.China, Jul. 25, 2017.

  • M. Abdulla, "Fine-Grained Reliability for V2X Communications," Future Network Theory Lab, 2012 Labs, Huawei Technologies Co., Ltd., Hong Kong Science Park, N.T., Hong Kong, Jul. 28, 2017. [The seminar was also broadcasted live to the Shenzhen Research Lab.] 

  • M. Abdulla, "Fine-Grained Reliability for V2X Communications," Communication Eng. Research Center, Key Lab. Oriented Intelligent Computation, School of Electronic and Information Engineering, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, Guangdong, P.R.China, Aug. 2, 2017.

 

 

 

 

 

□ Southeast Asia/ASEAN — Singapore

  • M. Abdulla, "Fine-Grained vs. Average Reliability for V2V Communications around Intersections," Ultra-Reliable Low-Latency Communications in Wireless Networks (URLLC), IEEE GLOBECOM'17, Marina Bay Sands Expo and Convention Centre, Singapore, Dec. 4, 2017.

  • M. Abdulla, "Fine-Grained Assessment of URLLC for V2X Communications," Smart Mobility Experience Lab (SMEx Lab), Centre for Infocomm Technology (INFINITUS), School of Electrical and Electronic Engineering (EEE), Nanyang Technological University (NTU), Singapore, Dec. 8, 2017.

 

● Outreach Efforts: We also disseminated our research and its social implications with the general public. In fact, we were invited by the organizing committee of Europe's leading popular science event (with 70,000 visitors), "The International Science Festival in Gothenburg" to co-organize and participate in various science and technology based activities and exercises, panel discussions, and outreach talks. As such, we brought R&D engineers from academia and industry working on next-generation 5G telecommunication systems, which will facilitate innovative technologies such as self-driving vehicles. The details of these events are chronicled below.

 

□ Hands-on Activities

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

*Special thanks to the following participants:

  • Ms. Malin Ulfvarson (Chalmers ICT)

  • Dr. Katrin Sjöberg (Volvo Group)

  • Dr. Sven Jacobsson (Ericsson Research)

  • Dr. Ayca Ozcelikkale (Chalmers S2)

  • Dr. Amina Piemontese (Chalmers S2).

□ Panel Discussions

□ Outreach Talks
     

 

News and words of encouragements about this project:  

  • S. Valji, "Prestigious Marie Curie Fellowship for Mouhamed Abdulla: Faculty of Engineering and Computer Science Graduate off to Sweden this Fall," Advancement and Alumni Relations, Concordia University, Jun. 18, 2015. Link 

  • Letter from Concordia University President and Vice-Chancellor, Prof. Alan Shepard, Jul. 15, 2015. Link 

  • Letter from Concordia University Dean, Prof. Paula Wood-Adams, Jul. 16, 2015. Link 

  • Interview with Chalmers University of Technology's INSIDAN, S2 Newsletter, Sep. 17, 2015. Link  

 
Activities: 

Over the period of the EU-H2020-MARSS-5G project we took part in various research and academic related activities. Some of these events are listed in the subsections below.

 

 

● Research Grants: Our research is supported, in part, by the following agencies and organizations.

 

□

EU-H2020-MARSS-5G Project, "Modeling and Analysis of Random Spatial Systems for 5G Networks," Marie Skłodowska-Curie Individual Fellowship (MSCA-IF-2014-EF), Grant No. 659933, European Commission, Brussels, Belgium, 2015 — Amount: € 173,857.20.
 
□

EU-H2020-HIGHTS Project, "High Precision Positioning for Cooperative ITS Applications," Research and Innovation Action: Cooperative ITS for Safe, Congestion-Free and Sustainable Mobility (MG-3.5a-2014), Grant No. 636537, European Commission, Brussels, Belgium, 2015 — Amount: € 5,999,616.25.
 
□

EU-H2020-is3DMIMO Project, "Indoor Small-Cell Networks with 3D MIMO Array Antennas," Marie Skłodowska-Curie Research and Innovation Staff Exchange (MSCA-RISE-2016), Grant No. 734798, European Commission, Brussels, Belgium, 2017 — Amount: € 1,309,500.00.
 
□

"5G-V2X Communications for Intelligent Transportation Systems," Chalmers Research Grant, Dept. of Electrical Engineering, Chalmers University of Technology, Göteborg, Sweden, 2016-2017 — Amount: 97,000.00 SEK.
 
□

"Ultra-Reliability for 5G Vehicle-to-Vehicle Communications," Ericsson Research Foundation, Grant No. FOSTIFT-16:043-17:054, Stockholm, Sweden, 2016-2017 — Amount: 58,000.00 SEK.

● Visit to Research Institutes: As part of the EU-H2020-MARSS-5G project and other EU funding, we had the opportunity to visit various research institutes. These visits included universities and corporations, located in different parts of the world, for seminars, meetings and research discussions. Overall, these visits have strengthen researcher-to-researcher connection, cooperation and interaction of ideas for pushing the boundaries of technical innovation.

 

□

Visiting Research Fellow, Dept. of Electronic Engineering, Tsinghua University, Beijing, P.R. China: July/Aug 2017.

  • This visit was supported by the EU-H2020-is3DMIMO project with focus on: spatial correlation of shadowing.

  • We had various meetings and discussions regarding 5G communications and ITS/VANET networks.

  • We also interacted with senior faculty members, postdocs, and graduate students, regarding technical topics, mathematical tools, and simulation practices.

  • We held meetings and exchanged research ideas with other visiting scholars from western universities, including Stanford University.

  • We were invited to give multiple talks to the communications research group, the EE department and visiting scholars regarding our most recent research work.

  • In addition to strengthening research ties between scholars in the East and the West, this extended research visit made us further appreciate the great traditions and history of the Chinese culture through visits to historical sites in the capitol Beijing.

  • Hosts: Prof. Yuan Shen (Research Institute of High-Speed Signal Processing and Network Transmission, Tsinghua Univ.), and Prof. Sheng Zhou (Research Institute of Telecommunications, Tsinghua Univ.).

 

□ Other Research Visits: Shorter visits (i.e. that lasted a week or less) to research institutes are listed below.

  • School of Information Tech., Halmstad Univ., Nov.11.2015 & Nov.2.2016 (Host: Prof. Elisabeth Uhlemann).

  • Dept. of Electrical & Computer Eng., Concordia Univ., Dec.16.2015 (Host: Dr. Anader Benyamin-Seeyar).

  • Electrical & Computer Eng. Dept., McGill Univ., Jan.5.2017 (Host: Prof. Fabrice Labeau).

  • School of Electrical Eng., KTH Royal Institute of Tech., May.18.2017 (Host: Prof. Lars Kildehřj Rasmussen).

  • 5G Standardization Group, China Mobile, Jul.15.2017 (Host: Ms. Yi Zhang, Beijing).

  • School of Electronic Eng., Beijing Univ. of Posts and Telecom., BUPT, Jul.20.2017 (Host: Prof. Li Wang).

  • Future Network Theory Lab, 2012 Labs, Huawei Hong Kong, Jul.27-28.2017 (Host: Dr. Bo Bai).

  • School of Electr. & Infor. Eng., Harbin Institute of Tech., Jul.30-Aug.2.2017 (Host: Prof. Yang Wang, HITSZ).

  • Dept. of Eng. & Information Tech., Univ. of Dubai, Sep.14.2017 (Host: Prof. Hussain Al-Ahmad).

  • Dept. of Electrical & Computer Eng., Univ. of Sharjah, Sep.17.2017 (Host: Prof. Sohaib Majzoub).

  • Dept. of Electrical Eng., ÉTS, Univ. of Québec, Oct.11.2017 (Host: Prof. René Jr. Landry).

  • School of Electrical & Electronic Eng., Nanyang Tech. Univ., Dec.5.2017 (Host: Prof. Yong Liang Guan).

● Distinguished Professors Invited to Chalmers: We hosted the following Professors to travel to Gothenburg/Sweden and to spend a week at the Dept. of Electrical Engineering of Chalmers University of Technology. As part of these visits, these distinguished scholars presented tutorial-style seminars on their area of expertise and their latest research work on 5G communications. We also had elongated discussions regarding our research on vehicular communications, and as a consequence of these exchanges, joint collaboration is underway.

 

□

Prof. Martin Haenggi, IEEE Fellow (University of Notre Dame, South Bend, IN, USA) — May. 2-6, 2016. Expertise: Stochastic Geometry.

 
□

Prof. Ke Wu, IEEE Fellow, IEEE MTT-S President (Polytechnique-MTL, Université de Montréal, Montréal, Québec, Canada) — Apr. 24-28, 2017. Expertise: Antenna Design.

 
□

Prof. Ekram Hossain, IEEE Fellow, IEEE VTS DL (University of Manitoba, Winnipeg, MB, Canada) — May. 15-19, 2017. Expertise: Resource Allocation.

 
□

Prof. Walid Saad (Virginia Tech, Blacksburg, VA, USA) — Jun. 19-23, 2017. Expertise: Game Theory.

 

 

 

● Organization of Technical Seminars:

 

□ EU-MARSS-5G & IEEE Sweden (R8-Europe) Sponsored Seminars

  • Walid Saad (Virginia Tech., USA), “The Internet of Everything: Context-Awareness, Drones, and V2X Networks,” Chalmers Univ. of Tech., Göteborg, Sweden, Jun. 21, 2017. Abstract

  • Ke Wu (Univ. of Montréal, Canada), “Enabling Ambient Electromagnetic Energy Harvesting for Future Internet of Things and Smart Environment,” Chalmers Univ. of Tech., Göteborg, Sweden, Apr. 27, 2017. Abstract

  • Ke Wu (Univ. of Montréal, Canada), “Multi-Dimension, Multi-Function and Multi-Band Substrate Integrated Waveguide Antennas and Arrays for GHz and THz Applications,” Chalmers Univ. of Tech., Göteborg, Sweden, Apr. 25, 2017. Abstract

  • Ekram Hossain (Univ. Manitoba, Canada), “Multi-tier Drone Cell Network: A New Frontier for 5G Research,” Chalmers Univ. of Tech., Göteborg, Sweden, May. 19, 2017. Abstract

  • Ekram Hossain (Univ. Manitoba, Canada), “Non-Orthogonal Multiple Access (NOMA) for 5G Wireless,” KTH Royal Institute of Tech., Stockholm, Sweden, May. 18, 2017.

  • Ekram Hossain (Univ. Manitoba, Canada), “Non-Orthogonal Multiple Access (NOMA) for 5G Wireless,” Chalmers Univ. of Tech., Göteborg, Sweden, May. 17, 2017. Abstract

  • Ekram Hossain (Univ. Manitoba, Canada), “On Coalition-Based Cooperative Packet Delivery in Vehicular Delay-Tolerant Networks Under Uncertainty,” Chalmers Univ. of Tech., Göteborg, Sweden, Sep. 12, 2016. Abstract  IEEE Sweden 

 

Organized IEEE Conference:

 

 

 

 

 

 

 

 

● Supervision of Graduate Engineering Students:

 

□

Various students took part in the EU-H2020-MARSS-5G project, including: 2 Industrial PhD + 3 MSc + 2 BSc. They each contributed to a particular aspect of the project. For more, please to the Team section on this page.
□

Former students are now working on applied engineering projects affiliated with Volvo Cars, RISE, Telia, etc. Some of our former M.Sc. and B.Sc. students are now pursuing higher-education in graduate schools in Sweden and abroad.
□

Students were recruited using ads posted on social media and on advertisement board around Chalmers. An example is shown here: .

 

● Teaching Activities: Although most of the EU-H2020-MARSS-5G project duration was devoted to research-related endeavors, we nonetheless contributed to teaching activities. This included lecturing of technical materials, attending teaching workshops, and exchanging with colleagues experiences on: teaching, learning, and course development.

 

□

Guest Lecturer, "SSY-135: Wireless Communications" graduate-level course, Dept. of Electrical Engineering, Chalmers University of Technology, Göteborg, Sweden, winter semester, 2017. Outline 

 
□

Moderator (WS3 session), "Entrepreneurial Experiences in Engineering Programs: What Is It And Why Should We Do It?," Chalmers Annual Conference on Teaching and Learning (KUL'17), Chalmers University of Technology, Göteborg, Sweden, Jan. 12, 2017. [The session is available on Page-8 ] 

 

● Participation in Conferences & Workshops: We participated in various technical conferences that took place abroad and in Sweden. These events provided us with insights on advances in modern technological innovation and fundamental research. We also found these venues beneficial for connecting and exchanging ideas with likeminded researchers.

 

□ International Conferences

  • The Royal Swedish Academy of Sciences, Nobel Prize Week Dialogue Conference on "The Future of Intelligence: AI", Svenska Mässan, Göteborg, Sweden, Dec. 9, 2015. 

  • IEEE ITSoc European School of Information Theory (ESIT'16), Göteborg, Sweden, Apr. 4-8, 2016.    [P.19]

  • IEEE Global Communications Conference (GLOBECOM'16), Washington DC, USA, Dec. 4-8, 2016.

  • IEEE SPS/EURASIP Summer School on Signal Processing for 5G Wireless Access (S3P'17), Göteborg, Sweden, May. 29-Jun. 1, 2017.

  • IEEE Global Communications Conference (GLOBECOM'17), Singapore, Dec. 4-8, 2017.
□ Swedish Conferences

  • IEEE VTS Society Workshop on Wireless Vehicular Communications (WWVC'15), Halmstad, Sweden, Nov. 11, 2015. 

  • IEEE/Chalmers Workshop on 5G Wireless and Vehicular Communications (CWVC'16), Göteborg, Sweden, May. 3, 2016.

  • IEEE VTS Society Workshop on Wireless Vehicular Communications (WWVC'16), Halmstad, Sweden, Nov. 2, 2016. 

  • IEEE Swedish Communication Technologies Workshop (Swe-CTW'17), Göteborg, Sweden, Jun. 1-2, 2017. 

□ Chalmers Conferences

  • Chalmers Communication Systems Group Workshop 2015 (CSWorkshop'15), Säröhus, Särö, Sweden, Oct. 26-27, 2015. 

  • Research Seminars, Chalmers Signals and Systems Day (S2-day'16), Göteborg, Sweden, May. 12, 2016. 

  • Chalmers Communication Systems Group Workshop 2016 (CSWorkshop'16), Hjortviken Konferens, Hindĺs, Sweden, Oct. 26-27, 2016.

  • Visit to the Visual Arena, Lindholmen Science Park, Göteborg, Sweden, Nov. 24, 2016. 

  • 7th Chalmers Annual Conference on Teaching and Learning (KUL'17), Göteborg, Sweden, Jan. 12, 2017.

  • Chalmers Initiative Seminar on "Digitalization: Opportunities and Challenges", Göteborg, Sweden, Mar. 15-16, 2017.

  • Research Seminars, Chalmers Electrical Engineering Day (E2-day'17), Göteborg, Sweden, May. 22, 2017. 

 

 

 

 

 

 

 

● Continuing Education on 5G Deployment: We attended various lectures and tutorials by industry researchers affiliated with major automotive and telecommunication companies working on real-world deployment. We also had the pleasure and opportunity to interact and discuss our research work on connected vehicles with some of these speakers.

 

□ Automotive

  • Dr. Katrin Sjöberg (Volvo Trucks/Sweden), "Platooning: Cooperative ITS & Active Safety," WWVC'15, Halmstad, Sweden, Nov. 11, 2015.

  • Dr. Erik Coelingh (Volvo Cars/Sweden), "Volvo Autopilot: the Technology that Makes the Car Drive Itself," S2-day'16, Göteborg, Sweden, May. 12, 2016.

  • Dr. Katrin Sjöberg (Volvo Trucks/Sweden), "C-ITS Deployment in Europe: Current Status and Outlook," WWVC'16, Halmstad, Sweden, Nov. 2, 2016.

  • Dr. John Kenney (Toyota InfoTechnology Center/SF, USA), "Dedicated Short Range Vehicular Communications - DSRC: Overview, Technical Challenges, and Applications," Washington D.C., USA, Dec. 8, 2016. Abstract
□ Network Infrastructure

  • Dr. Joachim Sachs (Ericsson Research/Sweden), "Vehicular Communications via Cellular Networks," WWVC'15, Halmstad, Sweden, Nov. 11, 2015.

  • Dr. Stefan Parkvall (Ericsson Research/Sweden), "4G, LTE, and the Road to 5G," Göteborg, Sweden, Apr. 18 & 21, 2016. 

  • Dr. Patrick Marsch (Nokia/Poland), "Nokia’s View on 5G Mobile Communications, and Specific 5G Challenges Addressed in Nokia Bell Labs Wroclaw," Göteborg, Sweden, Sep. 15, 2016. Abstract

  • Dr. Sara Mazur (Ericsson Research/Sweden), "5G: A Game Changer," Göteborg, Sweden, Mar. 15, 2017. Abstract

□ Mobile Chip

  • Dr. Edward Tiedemann (Qualcomm/SD, USA), "Big Steps in Wireless: Applications, Spectrum, and Technology," Washington D.C., USA, Dec. 5, 2016. Abstract

  • Dr. Michael Stetter (Intel/Munich), "5G Needs a Transformation of Wireless Landscape," Washington D.C., USA, Dec. 5, 2016. Abstract

  • Dr. Wonil Roh (Samsung/S.Korea), "5G: From Vision to Reality," Washington D.C., USA, Dec. 6, 2016. Abstract

 

 

 

 

 

 

 

 

 

 

 

 
Team: 

The following team members have contributed and collaborated to the EU-H2020-MARSS-5G project. The team is composed of senior scholars, industrial PhD candidates, and MSc students, with expertise in fundamental research, computational algorithms, design applications, empirical measurements, and data analysis. The particular specialization of each member is listed below:

 

Mouhamed Abdulla

Marie-Curie Fellow (PI)

Chalmers U. Tech.

Henk Wymeersch

Professor (Co-PI)

Chalmers U. Tech.

Andres A. Glazunov

Professor

Chalmers U. Tech.

Erik M. Steinmetz

Ph.D. Candidate

RISE

Srikar Muppirisetty

Ph.D. Candidate

Chalmers U. Tech.

Performance Evaluation

   

Network Analysis

Channel Propagation

V2V Communications

Predictive Modeling

Bjarki Vilmarsson

M.Sc., MPSYS

Chalmers U. Tech.

Daoyuan Yang

M.Sc., MPCOM

Chalmers U. Tech.

Suhail Ahmad

M.Sc., MPCOM

Chalmers U. Tech.

Rikard Reinhagen

B.Sc. Student

Chalmers U. Tech.

Martin Dahlgren

B.Sc. Student

Chalmers U. Tech.

System Design Tool

Design Application

Measurement Campaigns

Empirical Analysis

Hardware Configuration

 

 

 
Social Media: 

We regularly share updates of research projects on social-media. For more, you may follow and interact with us on the following platforms:

 

       
  For media inquiries or to setup an interview on connected/autonomous vehicles, please send an email to: ma14@ieee.org

Copyright © 2015-2022. All Rights Reserved. The EU-H2020-MARSS-5G project page is maintained by Mouhamed Abdulla